Risk and Reward in Fat Tails: Seizing Opportunities in Positive Kurtosis and Unpredictable Market Events

The statistical concept of positive kurtosis, also known as “fat tails,” describes probability distributions where extreme outcomes—those far from the mean—occur with significantly higher probability than predicted by standard models like the normal distribution. This phenomenon carries profound implications for financial markets, where rare but extreme events often dictate the risk and return landscape. The presence of fat tails means that traditional assumptions of risk, volatility, and predictability, grounded in linear or Gaussian models, may be inadequate or misleading.

As Nassim Taleb highlights in his foundational work, fat-tailed distributions invalidate many conventional methods in quantitative finance, such as in-sample estimates of means, variances, or linear regression-based relationships. These methods fail to accurately capture the heightened probability and disproportionate impact of outliers, which often dominate financial dynamics. This disconnect between traditional statistical tools and the realities of fat-tailed distributions creates inefficiencies and, potentially, opportunities for informed traders and risk managers to capitalize on market mispricing.

Kurtosis and the Shape of Risk

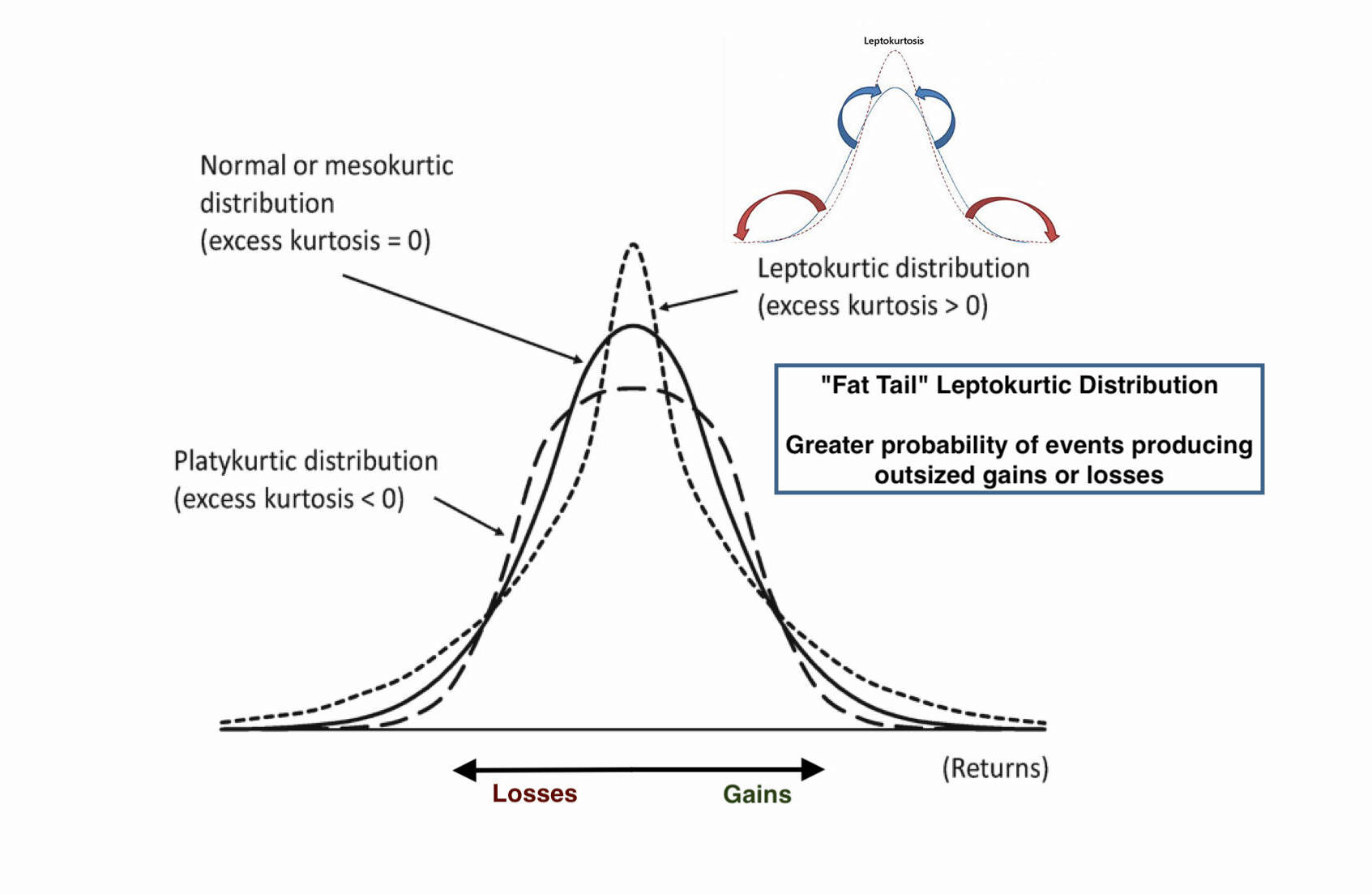
A key statistical measure of fat tails is kurtosis, which quantifies the probability of extreme outcomes. In essence, kurtosis measures the weight of the tails in a probability distribution, reflecting the likelihood of rare events occurring compared to a normal distribution. A normal distribution, for instance, assumes that 95% of all values lie within two standard deviations of the mean. However, in distributions with high kurtosis, the probability of extreme deviations increases, leading to "fatter" tails.

The visualization of kurtosis often uses the familiar bell curve, where the bulk of observations cluster around the center, while extreme values taper off into tails. When kurtosis is elevated, the tails are disproportionately large, and the central peak often sharpens, reflecting an increased concentration of data near the mean. This phenomenon fundamentally alters risk assessments, as it suggests a heightened likelihood of both extreme losses and extreme gains.

Mathematical Definition

Kurtosis (K) is formally defined as:

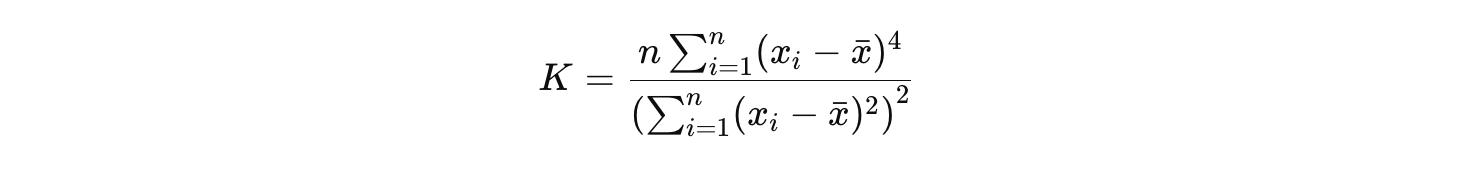
Where:

• n is the number of observations
• xi represents individual data points
• x̄ is the mean of the data

For a normal distribution, kurtosis equals 3, a baseline often referred to as "mesokurtic." Distributions with kurtosis greater than 3 are "leptokurtic" (fat-tailed), while those with kurtosis less than 3 are "platykurtic" (thin-tailed).

Real-World Example: Fat-Tailed Distributions in Financial Markets

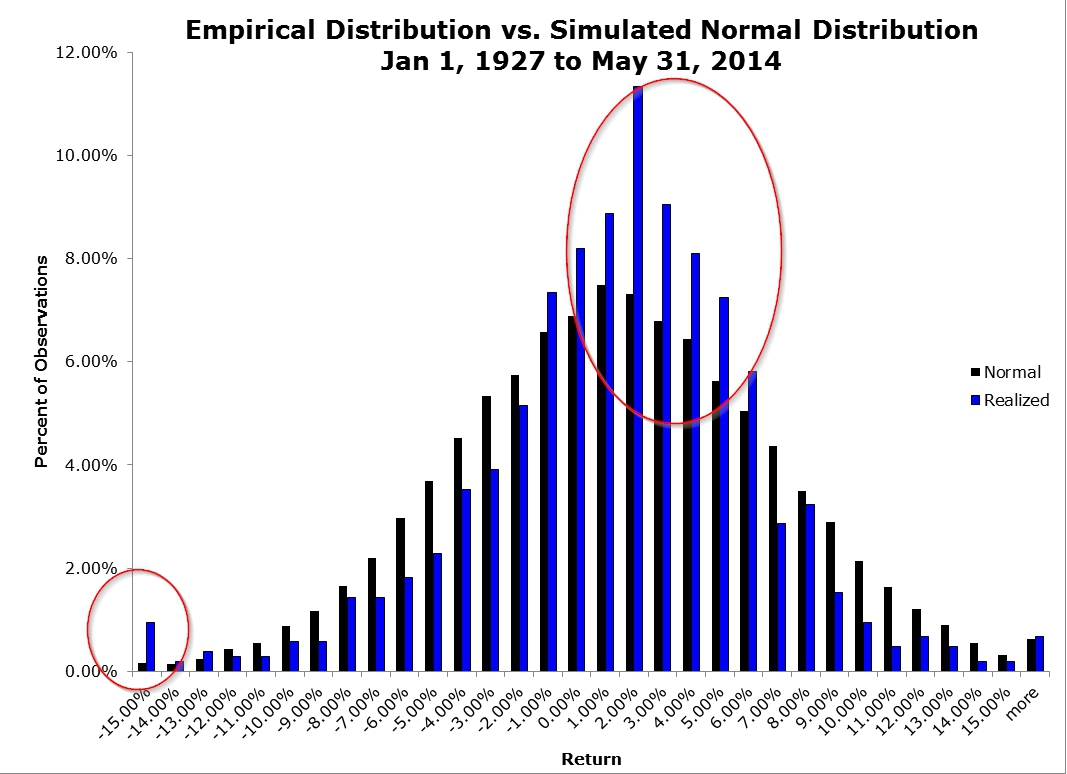
Fat tails manifest clearly in financial markets, where extreme price movements often defy traditional Gaussian assumptions. Tail risk refers to the probability of extreme deviations in asset prices—either significantly positive or negative—beyond the expected range of outcomes. A practical illustration can be seen by analyzing the daily returns of an asset. If we plot these returns on a histogram, most observations will cluster around a narrow range near zero, representing minimal daily changes.

However, the extreme left and right tails of the distribution—corresponding to significant market crashes or surges—will exhibit a disproportionately higher frequency than predicted by a normal distribution. Statistically, tail risk lies at the distribution's edges, or “tails,” where rare but impactful events reside. These risks, though infrequent, can disrupt markets, portfolios, and economies, making their management a critical focus for practitioners.

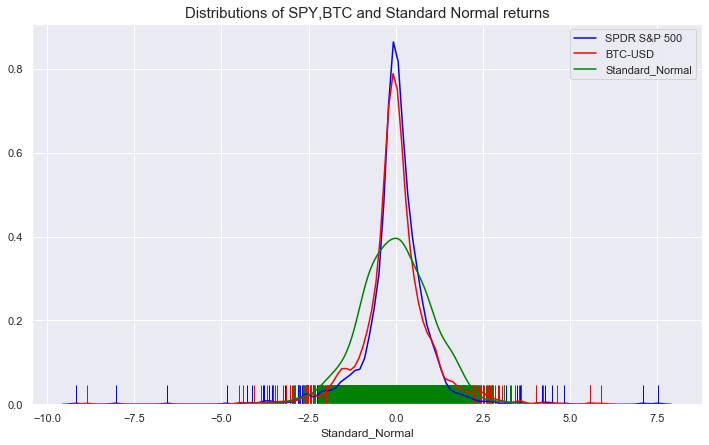
For instance, consider the historical returns of equity markets during the 2008 financial crisis or the rapid collapses observed during the COVID-19 pandemic. Both events illustrate how fat tails dominate risk and return profiles. Markets experienced single-day losses and gains that exceeded six standard deviations—events so rare under normal assumptions that they would theoretically occur only once in millions of years, yet they materialize with troubling regularity in real markets.

Elevated Kurtosis in Recent Events

The current environment seems to be marked by higher kurtosis, reflecting a greater frequency and impact of extreme, unexpected events. Recent examples underscore how consensus predictions, such as opinion polls, have failed to anticipate these outcomes accurately.

Misjudged Expectations: U.S. Presidential Election
The 2016 and 2024 U.S. Presidential election is a vivid illustration of heightened kurtosis. Pre-election opinion polls—intended to capture consensus expectations—clearly underestimated the likelihood of Donald Trump’s victory. The low-probability outcome became reality, highlighting the fragility of traditional forecasting methods in the face of complex, multifaceted dynamics.

Following the election, markets exhibited a remarkable rally, defying initial expectations. Investors quickly adapted to the unexpected result, recalibrating their focus toward potential economic benefits such as:

• Proposed tax cuts
• Trade protectionist policies
• Deregulation in energy and financial sectors

This swift adjustment suggests that investors, when faced with fat-tail events, often pivot to emphasize potential positive outcomes—even if such optimism is speculative or tenuous.

The Case for a Micro Approach Over Macro

Within the hedge fund universe, global macro strategies—which involve betting on broad economic or geopolitical trends—have historically attracted significant attention. Recent years have provided ample opportunities for macro plays, including elections, Federal Reserve policy changes, and major currency fluctuations.

Underperformance of Macro Strategies

Despite these opportunities, in 2024, global macro strategies have underperformed relative to other hedge fund strategies. For example:

• Quantitative and equity long/short strategies outperformed significantly, with returns of +8.2% and +6.1%, respectively, year to date.
• Global macro strategies lagged, posting a modest +3.5%, behind even the hedge fund industry average.

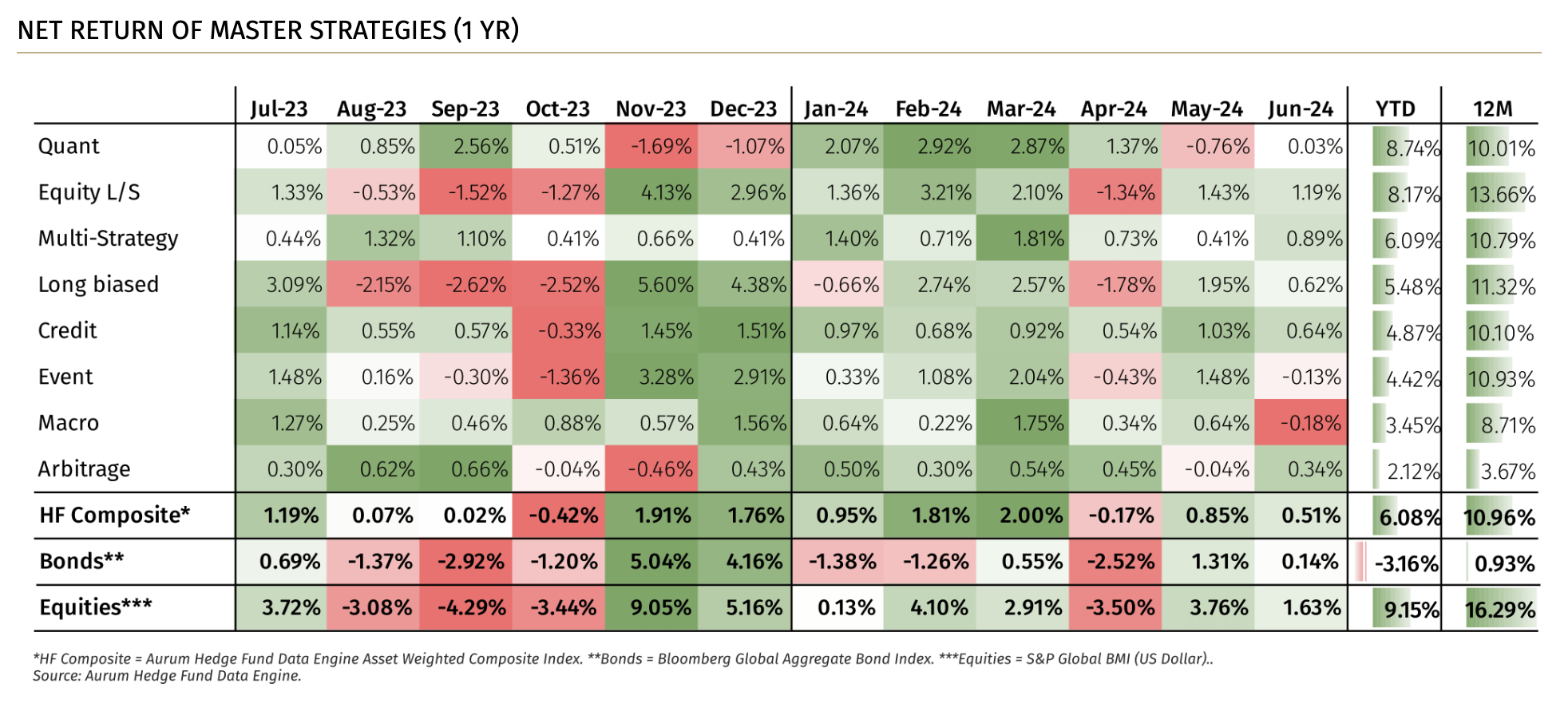
The underperformance of macro strategies can be attributed to several factors. Firstly, macro events often lie deep in the "tails" of normal distributions, making them inherently unforecastable. These tail risks, which involve rare but impactful occurrences, are difficult to predict and can result in significant market shifts that traditional models fail to capture.

Additionally, low-interest rates and excess liquidity have further impeded the effectiveness of macro strategies by suppressing volatility and distorting traditional market signals. These conditions reduce the clarity of market trends and make it harder for macro strategies to react effectively, leading to underperformance in many cases.

A Pragmatic Investment Philosophy

A more pragmatic investment philosophy shifts the focus away from attempting to predict broad macro trends, instead emphasizing company-specific fundamentals—an area where research has a higher likelihood of success. This philosophy lies at the heart of many hedge fund strategies, particularly long/short equity-oriented funds, which prioritize:

• Identifying the key drivers of company performance
• Understanding sector-specific dynamics
• Uncovering mispricings that can be systematically exploited

While stock-specific research is not infallible, even a slight edge in accuracy—such as being right just over 50% of the time—can lead to outsized returns. Research suggests that a 55% accuracy rate in stock selection can lead to an annual outperformance of 3–5% relative to the broader market. Moreover, during periods of heightened market volatility, sector-focused strategies have historically outperformed broader indices by 10–15%, showcasing the potential for significant returns from micro-level research.

In an investment landscape shaped by fat tails, this approach provides a strong advantage, as it allows investors to better steer through the unpredictable nature of macroeconomic and geopolitical forces with greater agility and precision.

Applications to Risk Management

In financial markets, risk management relies heavily on accurate calculations to estimate a portfolio’s or trade’s exposure to uncertainty. However, the presence of fat tails in financial market returns fundamentally challenges the reliability of traditional risk metrics. These metrics often fail to fully account for the heightened probability and outsized impact of extreme events, as such events are frequently driven by unknown or unpredictable factors that elude conventional modeling.

Addressing Extreme Risks with Power-Law Models

Power-law models offer a superior framework for risk management, as they more accurately represent the probability distribution of extreme losses. Unlike Gaussian-based models, which assume thin tails and underestimate the occurrence of rare events, power-law distributions incorporate the fat-tailed nature of returns, enabling more realistic assessments of risk exposure.

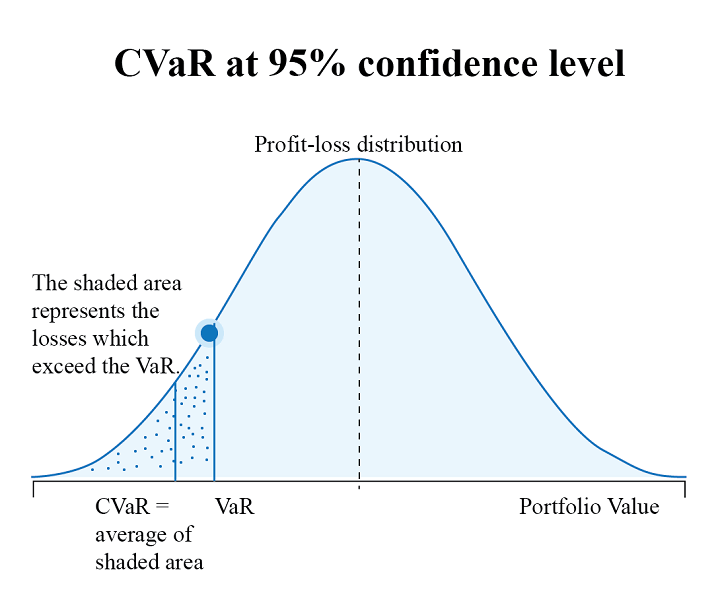
For example, metrics such as Conditional Value at Risk (CVaR) are particularly effective in quantifying tail risks under scenarios of market crashes or black swan events, as they focus on the severity of losses in the worst-case scenarios. Research indicates that traditional Value at Risk (VaR) models underestimate potential losses during extreme events by as much as 30–50%, highlighting the importance of adopting power-law frameworks. In a power-law context, CVaR can be expressed as:

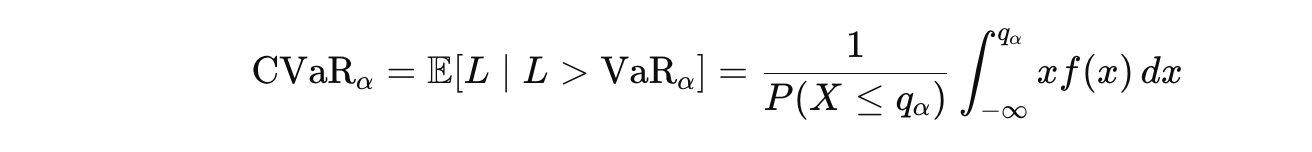
Where:

• CVaRα is the Conditional Value at Risk at confidence level α,
• L represents the loss random variable,
• VaRα is the Value at Risk at confidence level α,
• qα is the quantile corresponding to α,
• f(x) is the probability density function of X.

An example illustrates the significance of using power-law distributions: During the 2008 financial crisis, losses on equity indices exceeded thresholds predicted by Gaussian models, leading to widespread portfolio failures. Power-law models, however, accurately predicted the higher probability of such extreme losses, enabling better preparedness.

Moreover, power-law distributions aid in stress-testing portfolios under extreme scenarios. By simulating tail-heavy events, risk managers can assess the potential impact of outliers on portfolio performance. For instance, under a power-law framework, a portfolio exposed to assets with tail index alpha < 2 may exhibit infinite variance, highlighting the need for strict risk controls and diversification strategies tailored to fat-tailed risks.

Incorporating power-law insights empowers traders and risk managers to develop more resilient strategies, such as tail-hedging using options or derivatives that gain value during extreme market downturns. This proactive approach not only mitigates downside risks but also opens the door to leveraging rare opportunities, turning fat tails from a liability into a strategic advantage.

Optimizing Algorithmic Risk Controls

Algorithmic risk controls can be significantly improved by integrating power-law principles. Traditional algorithms often rely on static stop-loss thresholds, which may fail to react effectively to sudden and extreme price movements, leading to underperformance or even catastrophic losses.

By adopting power-law-adjusted thresholds, algorithms can better capture the dynamics of rare events, creating more resilient and adaptive systems. This adjustment reduces vulnerability to abrupt, extreme shocks and equips trading systems to manage risks proactively in the face of uncertainty.

Simulations show that power-law-based algorithms can decrease drawdowns during market turbulence by up to 20% compared to traditional models, underscoring their value in volatile conditions.

Profit Potential of Fat Tails: Strategies for Capturing Rare Market Events

Fat tails create a paradox for traders: they can lead to either extreme losses or substantial profits, depending on how risk is structured and managed. To capture the positive potential of fat tails while minimizing exposure to catastrophic downside risks, traders must adopt strategies that account for rare but impactful events. This approach is essential as financial markets often experience significant deviations from the norm, with events in the tails of distributions—those that have low probability but high impact—being more frequent than traditional models suggest.

Adapting Trading Models to Fat Tails

Trading models, particularly those used for portfolio optimization and asset allocation, must be adapted to account for fat-tailed distributions. Incorporating power-law distributions adjusts expectations for both returns and risks, striking the balance between risk and reward.

According to Bessembinder (2018), about 80% of the stock market's total returns come from only 20% of the events, many of which fall in the fat tail of the distribution. These adjustments necessitate a reassessment of risk appetite and the development of robust strategies designed to handle extreme outcomes, both positive and negative. This is increasingly critical as financial markets remain susceptible to rare, high-impact events.

Tail-Aware Trading Strategies

One effective way to manage fat-tail risks is through tail-aware strategies, such as the barbell approach. In this approach, a portfolio is largely allocated to low-risk, stable assets, while a small portion is reserved for high-risk, high-reward opportunities. This strategy allows traders to take advantage of the extreme profits offered by the fat tails while protecting themselves from catastrophic losses.

Example: If 80% of the portfolio is invested in low-risk, stable assets and 20% is dedicated to high-risk assets, the potential for large profits during rare, extreme events is captured, while losses from market crashes are minimized. This strategy effectively balances the dual challenges of managing tail risks and rewards, positioning traders to exploit rare events without undue exposure to risk.

Enhancing Quantitative Models with Fat-Tail Insights

Incorporating fat-tail insights into quantitative models further strengthens trading strategies. For example, high-frequency trading (HFT) strategies, which are prone to volatility shocks, can benefit from integrating power-law distributions to anticipate disruptions and adjust portfolios dynamically. This enables real-time portfolio adjustments, preventing significant losses during sudden market shifts.

Data Insight: During market shocks, trading algorithms that do not account for fat tails often experience up to a 20% higher loss compared to those that integrate fat-tail risk models. By adjusting return projections and incorporating fat-tail risks, trading models become more resilient, maintaining stability even during volatile episodes that would typically disrupt traditional models.

Optimizing Signal Generation for Algorithmic Trading

Algorithmic trading systems rely heavily on signal generation models, which often assume stable and predictable returns. However, these assumptions break down in the presence of extreme, fat-tailed events. By integrating power-law principles, algorithms become more dynamic and able to respond to rare shocks with greater precision.

Example: Momentum-based algorithms adjusted to recognize fat-tail probabilities can better calibrate risk-on and risk-off signals, reducing drawdowns during volatile periods. For instance, a signal may trigger to reduce exposure by 15–20% when an extreme event is forecasted, helping the portfolio avoid large losses.

Machine learning-based models trained on data with power-law distributions also learn to account for both frequent occurrences and rare, impactful events, producing strategies that are robust in both normal and extreme market conditions. This is key, as algorithms adjusted for fat tails can respond swiftly to price shocks, leading to improved performance.

Conclusion

Fat tails in financial markets present both a formidable challenge and an extraordinary opportunity. Their inherent unpredictability complicates traditional risk assessment and trading strategies, but their influence is inescapable. Rather than being paralyzed by the uncertainty they introduce, traders and risk managers must adopt a proactive approach that not only mitigates their downside but also leverages their upside.

The invisible tail of power-law distributions compels a reexamination of how we quantify and manage risk. Conventional models, with their reliance on Gaussian assumptions, fail to account for the frequency and magnitude of extreme events. This gap necessitates the use of more robust tools, such as power-law-based metrics, which enable a more realistic representation of risks and opportunities. By redefining how we perceive metrics like mean, variance, and value at risk, these tools provide a clearer understanding of the impact of rare, high-magnitude events.

For risk managers, the task goes beyond refining calculations; it involves creating systems and strategies resilient enough to withstand market turbulence. Meanwhile, traders and algorithm developers who integrate tail-aware principles into their models can anticipate and react to volatility more effectively. Whether through adaptive signal generation or barbell strategies, these approaches transform the unpredictable nature of fat tails from a liability into a strategic advantage.

Ultimately, the key lies in recognizing the dual nature of fat tails—acknowledging their risks while positioning to capitalize on their rare opportunities. By doing so, we can shift from merely surviving extreme market events to thriving amid them, turning uncertainty into a powerful driver of long-term success.